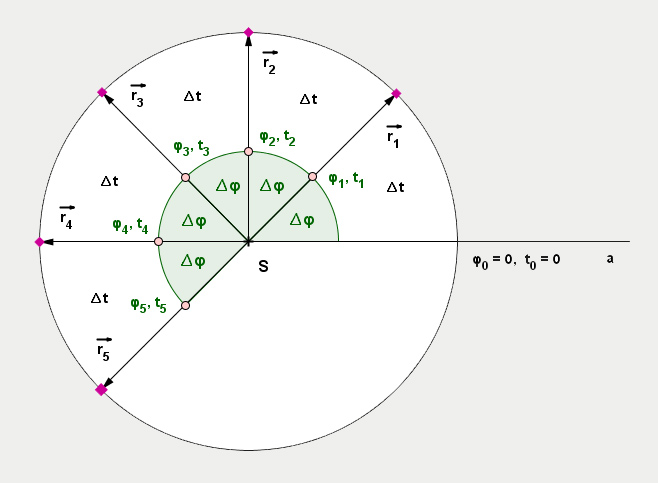
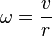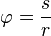Pohyb po kružnici
je špeciálny druh krivočiareho pohybu, kto
rého trajektóriou je kružnica (časť kružnice)Všeobecný (nerovnomerný) pohyb po kružnici - veľkosť rýchlosti sa mení inak ako lineárneRovnomerne zrýchlený pohyb po kružnici - veľkosť rýchlosti sa mení priamo úmerne s časom (zrýchlenie je konštantné).
Rovnomerný pohyb po kružnici - nemení sa veľkosť rýchlosti (rýchlosť je konštantná). Poloha hmotného bodu pri pohybe po kružnici V polárnej sústave súradníc
- r = \mathrm{const.} \,
- \varphi = f(t)
V karteziánskej sústave súradníc
- x = r \cos(\varphi + \varphi_0)
- y = r \sin(\varphi + \varphi_0)
kde
- r — je polomer kružnice v (m)
- t — je čas v (s)
- φ — je uhlová dráha v (rad)
- x, y — sú karteziánske súradnice polohy v (m)
Perióda a frekvencia
Perióda je doba, za ktorú hmotný bod opíše kružnicu jedenkrát.
- T = \frac{2 \pi}{\omega} ;\qquad T = \frac{2 \pi r}{v}
Frekvencia určuje počet kružníc, ktoré hmotný bod prejde za jednotku času.
- f = \frac{\omega}{2 \pi} ;\qquad f = \frac{v}{2 \pi r}
Výpočet pohybu po kružnici

kde
- ω — je uhlová rýchlosť v (rad/s)
- ω0 — je počiatočná uhlová rýchlosť (uhlová rýchlosť v čase t=0) v (rad/s)
- φ — je uhlová dráha v (rad)
- φ0 — je počiatočná uhlová dráha (uhlová dráha v čase t=0) v (rad)
- t — je čas v (s)
- ε — je uhlové zrýchlenie v (rad/s²)
Vzťahy uhlových a obvodových veličín
- uhlová rýchlosť
- uhlová dráha
kde
- v — je obvodová rýchlosť v (m/s)
- s — je obvodová dráha v (m)
- r — je polomer kružnice v (m)
Silové pôsobenie
Dostredivé zrýchlenie je vyvolané dostredivou silou, ktorej smer je do stredu kružnice. Pri rovnomernom pohybe po kružnici sa jej veľkosť nemení. Z 2. Newtonovhopohybového zákona je veľkosť dostredivej sily:
kde
- m — je hmotnosť hmotného bodu v (kg)
- ω — je uhlová rýchlosť v (rad/s)
- r — je polomer kružnice v (m)
- v — je obvodová rýchlosť v (m/s)
Dostredivá sila má svoju reakciu v odstredivej sile, ktorej veľkosť je rovnaká, ale pôsobí smerom od stredu kružnice.